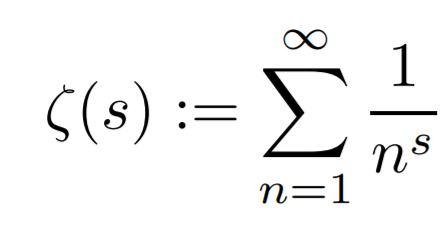In this post I want to talk about why providing good and detailed explanations can be a key in deep understanding of things in different fields of life. Particularly, I want to talk about detailed proofs in mathematics that have good step by step explanations of how the proof was constructed. Recently, I’ve started to read the books on math that are piling on my table just as the image above depicts.
I want to point your attention to the second book at the top of the pile, which is Prime Numbers and the Riemann Hypothesis book from 2016 written by Barry Mazur and William Stein. This book talks about Riemann Hypothesis by starting from ‘simple’ math and gradually moving to details about Riemann Hypothesis that require more advanced math background.
So what levels of understanding and well explained proofs have to do with the content of the book. Well, you see in the first part of the book, which authors claim requires some minimal math background a read sees this
Here are two exercises that you might try to do, if this is your first encounter with primes that differ from a power of 2 by 1:
1. Show that if a number of the form M = 2^n – 1 is prime, then the exponent n is also prime. [Hint: This is equivalent to proving that if n is composite, then 2^n -1 is also composite.] For example: 2^2 – 1 = 3, 2^3 -1 = 7 are primes, but 2^4 – 1 = 15 is not. So Mersenne primes are numbers that are
– of the form 2^ prime number – 1, and
– are themselves prime numbers
Some context for the quote
Here comes a little bit of a context about this quote. The quote comes from, part 1, chapter 3: ‘”Named” Prime Numbers’, on page 11. The chapter describes what are Mersenne Primes, which are prime numbers that are one less than a power of two:
M = 2^n – 1
Also, it’s good to know that a prime number is a whole number (positive integer) that can be divided only by itself or 1. For example,
2, 3, 5, 7, 11 … are prime numbers since they can only be divided by themselves and 1.
Now, that we know what prime numbers are, I want to draw your attention to the point in the quote where it says, that the exercises are good for ‘your first encounter with primes that differ from a power of 2 by 1‘. Well, in my opinion these exercises are good only for readers who have at least a BSc in Math or possibly an engineering degree. In a couple of sentences we’ll see why I think so. Since I consider myself as a person who is interested in math and have a BSc degree in Electronics, I think the first part of the book which is indented for a layman person is just for me. Were you able to arrive at the proof for that simple exercises above?
Frankly, I wasn’t able to prove it. So, I went and looked for a proof on the internet. As always, Wikipedia is at the top of the Google search when it comes to math topics. Lo and behold there is a page in the wiki about Mersenne primes, what they are and a number of proofs related to them. One of the proofs was exactly the solution to the exercise in the quote above. Here it comes:

Note: Since, I had no time to learn how to use LaTeX properly in the WordPress, and believe me WordPress doesn’t make blogger’s life easy I write the proofs and picture them.
Does this proof looks like a piece of cake to you? Is it intuitive and easy to grasp? In my opinion, it’s not and also this proof shows why Wikipedia gets a good portion of criticism about its content.
What I find not so obvious about that proof is how the right hand side of the equation came about. Especially, the part that has powers of a * (b – 1) , a* (b – 2), … , a, 1. And then the statement that says ‘By contrapositive, if 2^p -1 is prime then p prime‘. In this particular statement, if you had no courses on mathematical proof, logic or Abstract Algebra, then the words composite and contrapositive can be a little bit mysterious.
I thought to myself, well, the proof looks kind of unclear to me, so I searched better using the internet and also checked the books I own. I was able to find a couple of proofs that were easier to understand and also was able to find a proof in the Book of Proof by Richard Hammack that you can see in the title image for the post. It’s the blue one and it comes third from the top of the pile.
Let’s start with the proof from the Book of Proof, which sounds like a good place to begin with. The proof is a solution to the exercise 25 from Chapter 5 in the book.
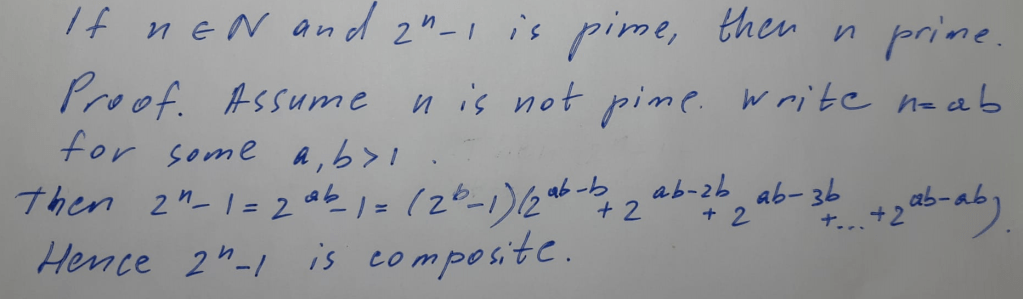
If we look carefully at this proof it look almost exactly as the proof in the Wikipedia. It even look less clear. But one important thing to notice is that this proof shows where the ‘1’ comes from on the right hand side of the equation, in comparison to the proof in the wiki. I think so, since 2^(ab-ab) which equals 1, provides more information than a simple number 1. This is because it provides some clues on how the proof was constructed. But for a reader who does not remember math, both of the proofs are not that helpful. Also, we need to take into consideration, that the Book of Proof intended audience is undergraduate students of exact sciences. So the book presupposes some math background.
Some math background
We already mentioned that a prime number is a positive integer that can be only divided by itself or number 1. All other integers, are composite, since any of them can be composed by multiplying prime numbers. This is where composite comes from. As for contrapositive the Merriam-Webster site provides this definition
a proposition or theorem formed by contradicting both the subject and predicate or both the hypothesis and conclusion of a given proposition or theorem and interchanging them
if not-B then not-A ” is the contrapositive of “if A then B ”
For example,
If it was raining then it is wet.
Then contrapositive statement would be
If it is not wet then it wasn’t raining.
Returning back to the original exercise from the Prime Numbers and the Riemann Hypothesis book, now, it becomes a little bit clear, what the hint [Hint: This is equivalent to proving that if n is composite, then 2^n -1 is also composite.] there was for. So the proofs, went to prove that
If n is composite then 2^n – 1 number is composite
and by contrapositive
If 2^n – 1 number is not composite (i.e. prime) then n is not composite (i.e. prime)
Polynomial factorization
Now, that we know what contrapositive proof is that’s turn to the right hand side part of the equation which is
2^n – 1 = (2^a – 1) * ( 2^a*(b-1) + 2^a*(b-2) + … + 2^a + 1).
It turns out that to derive it there is need to remember what polynomial factorization is, or remember how to divide one polynomial by another, or to know what Polynomial remainder theorem is. Also it’s good to know for a start what is a polynomial.
Since this post is becoming to long I need to make it shorter, which defeats the point of providing detailed explanations 😦
But I’ll provide some hints on how the right hand side was derived.
There is a known math formula to compute the following expression a^n – b^n
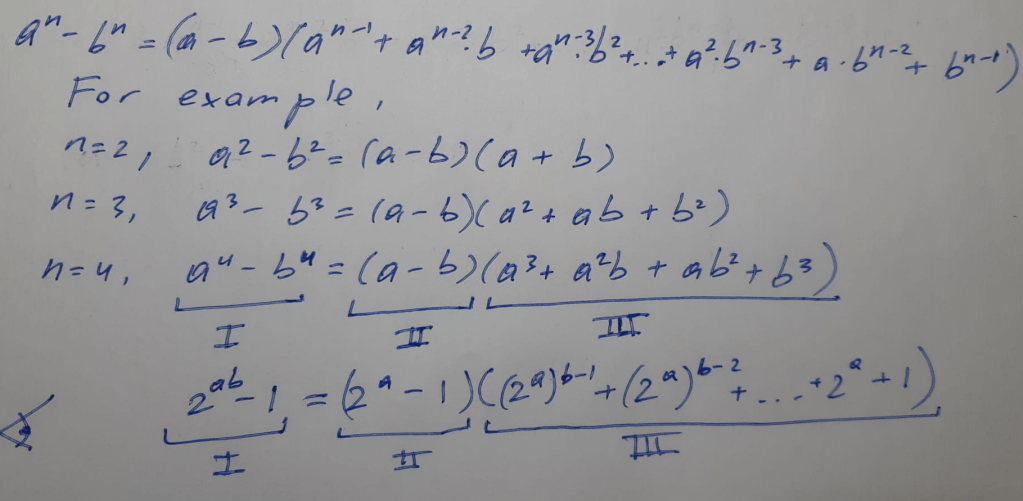
It turns out that the equation in the proofs that were mentioned in this post has the same structure as the formula to derive a^n – b^n. But the most interesting part is this. If you look at the last equation the Roman numeral I stands for the initial composite number 2^n – 1, and it is composed by multiplying Part II by Part III.
Part I = Part II * Part III
What is interesting about this composite number and that me use A, B and C instead of using I, II and III
A = B * C
is that B and C are factors of A, or alternatively B is a divisor and C is a quotient.
So to summarize the initial number 2^n -1 is composite since it is a product of two other numbers.