As it sometime happens to me while I was checking what’s new on YouTube the suggestions algorithm had a video about Memristor which was a forth basic electrical element that had a memory in it. While I was watching that interesting video that was created by prof. Giordano Scarciotti I saw the symmetry diagram that prof. Leon Chua came up with back in 1971. In that paper he proposed Memristor as a missing fundamental component in electrical circuit theory. So, what’s interesting about that diagram that it very much resembles diagrams in Category Theory.

Next, I’ve used Windows Copilot to elaborate on that idea. Chatting with it back and forth resulted in the blog post below:

Introduction

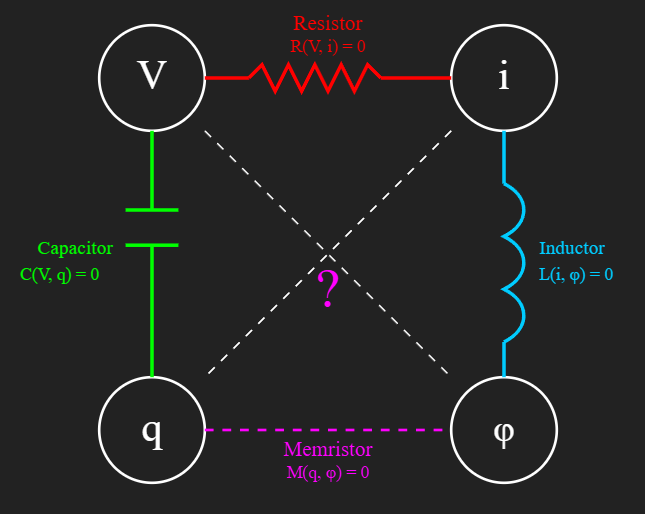
When we first learn electronics, we’re introduced to three fundamental passive elements: the resistor, the capacitor, and the inductor. Each one ties together two physical quantities:

• Resistor: relates voltage V and current i.
• Capacitor: relates voltage V and charge q.
• Inductor: relates current i and magnetic flux φ.

But in 1971, Leon Chua predicted a missing fourth element — the memristor — which connects charge q and flux φ. This completed the symmetry among the four fundamental electrical quantities.

🔎 Constitutive Relations and the “=0” Notation

In advanced circuit theory, each element is defined by a constitutive relation: a constraint between two variables. Instead of writing explicit formulas like Ohm’s Law (V = R·i), theorists often use an implicit form:

• Resistor: R(V, i) = 0
• Capacitor: C(V, q) = 0
• Inductor: L(i, φ) = 0
• Memristor: M(q, φ) = 0

This doesn’t mean resistance is zero. It means: the pair of variables must satisfy some relation enforced by the element. For a linear resistor, that relation is V − R·i = 0. For nonlinear devices, the relation could be more complex. The implicit form is powerful because it generalizes to nonlinear, time-varying, and memory-dependent behaviors.

🔄 Symmetry and Completeness

Chua’s insight was that with four fundamental quantities (V, i, q, φ), there should be six possible pairings. Three were already realized by resistor, capacitor, and inductor. The missing link — charge to flux — was filled by the memristor. This symmetry is what makes the framework elegant: every pair of quantities is connected by a constitutive relation.

🧩 A Category-Theoretic Perspective

Here’s where the categorical flavor comes in. The symmetry looks a lot like category theory:

• Objects: The four quantities (V, i, q, φ).
• Morphisms: The four elements (resistor, capacitor, inductor, memristor).
• Composition: Just as morphisms compose in category theory, circuit elements combine to form networks.
• Commutativity: The square diagram commutes:
  L ∘ R = M ∘ C
  meaning that whether voltage is mapped to flux via current (resistor → inductor) or via charge (capacitor → memristor), the structural mapping is consistent.

🖼️ ASCII Diagrams

Fundamental Square of Relations

   V ──R──▶ i
   │        │
   C        L
   │        │
   ▼        ▼
   q ──M──▶ φ

• R : V → i (Resistor)
• C : V → q (Capacitor)
• L : i → φ (Inductor)
• M : q → φ (Memristor)

Commutative Diagram

        V
       / \
      R   C
     /     \
    i       q
     \     /
      L   M
       \ /
        φ

Here, the two paths from V to φ are equivalent:
L ∘ R = M ∘ C

✨ Why This Matters

Thinking categorically opens new doors:

• Circuits can be modeled as categories of physical quantities.
• Functorial translations could connect circuit categories to computational categories (logic, automata).
• Neuromorphic computing, where memristors play a central role, might benefit from categorical semantics.

The memristor isn’t just a missing device — it’s the morphism that makes the diagram commute, completing the symmetry both physically and mathematically.

🧠 The Main Idea

By reframing Chua’s symmetry in categorical terms, we see circuits not just as physical devices but as mathematical structures. The memristor completes not only the physics of passive elements but also the mathematics of a commutative square.

This perspective — born from blending electronics with category theory — is a fresh, original way of thinking about circuit theory. It shows how abstract mathematics can illuminate engineering, and how symmetry drives discovery.